REMEDIAL PAT matematika(RAISYA ALIA YUSARIN XI IPS1)

 Nama: Raisya Alia Yusarin

Kelas: XI IPS 1

Absen:29

REMEDIAL PAT MATEMATIKA 

REMEDIAL PTS 1-25

Nama: RAISYA ALIA YUSARIN

Kelas: XI IPS 1

Absen: 29

Tanggal dikumpulkan: Rabu,5 April 2023

IV. INTEGRAL FUNGSI ALJABAR

 NAMA: RAISYA ALIA YUSARIN

XI IPS1/29

MATEMATIKA SEMESTER GENAP

A. INTEGRAL TAK TENTU

Integral merupakan operasi kebalikan dari diferensial atau biasa disebut juga dengan antidiferensial. Salah satu bentuk integral yakni integral tak tentu.

Rumus Integral Tak Tentu

Untuk mengerjakan soal integral tak tentu, perlu diketahui rumusnya terlebih dahulu.

Keterangan:

ʃ = operasi antiturunan atau lambang integral

C = suatu konstanta real

f(x) = turunan (diferensial) dari f(x) + C

Sifat-Sifat Integral Tak Tentu
Adapun untuk mengenali contoh soal integral tak tentu, wajib memahami sifat-sifat integral tak tentu. Di antaranya:

https://www.detik.com/edu/detikpedia/d-5616363/contoh-soal-integral-tak-tentu-dan-pembahasannya

contoh soal
 Tentukan hasil dari ʃ 3x2 dx !

Jadi, hasil dari ʃ 3x2 dx adalah x3 + C.

https://rumuspintar.com/integral/contoh-soal/

B. TEKNIK PENGINTEGRALAN

Teknik Integral Substitusi

Integral Substitusi adalah sebuah metode atau teknik dalam menyelesaikan masalah integral. Sesuai namanya, kita menggunakan substitusi untuk menyederhanakan masalah.Jika sebuah persamaan integral begitu kompleks, maka dibutuhkan teknik substitusi untuk menyederhanakannya. Rumus integral subtitusi adalah sebagai berikut:

Teknik Integral Parsial

Integral parsial digunakan dengan memisahkan dua fungsi berbeda, tetapi memiliki variabel yang sama. Rumus integral parsial adalah sebagai berikut:

di mana f(x) = u, sehingga du = f(X)dx; dan g(x) = v, sehingga dv = g(x)dx.

https://www.medcom.id/pendidikan/news-pendidikan/GKdjynXb-mengenal-konsep-integral-jenis-teknik-penyelesaian-dan-contoh-soal

CONTOH SOAL INTEGRAL SUBTITUSI

https://mathpro.id/pembahasan-soal/integral-substitusi

C. SOAL YANG BERHUBUNGAN DENGAN INTEGRAL

Contoh Soal Integral Tak Tentu

Soal 1

Pembahasan

Contoh Soal Integral Tentu

Contoh soal integral tentu. (Arsip Zenius)

Pembahasan

Contoh Soal Integral Trigonometri

Soal integral trigonometri. (Arsip Zenius)

Pembahasan

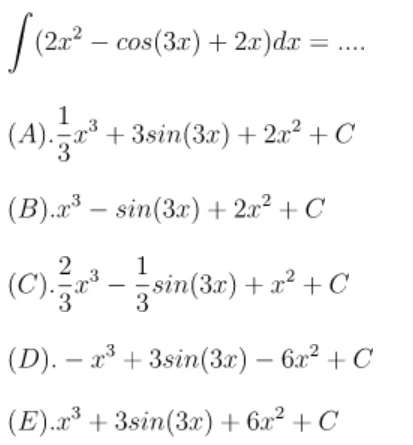
Pembahasan soal integral trigonometri. (Arsip Zenius)

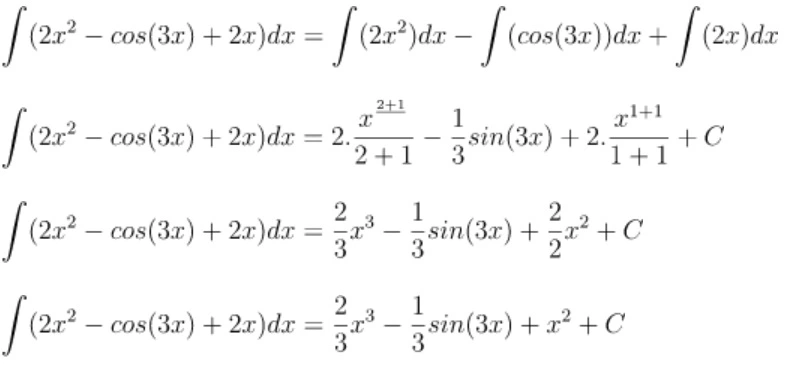
Jadi, jawabannya adalah C.

Contoh Soal Aplikasi Integral

Soal 1

Contoh soal aplikasi integral. (Arsip Zenius)

Pembahasan

Diketahui, f’(x) = 5x-2 dan f(2) = 12.

Yang ditanya adalah f(x), maka:

Pembahasan soal aplikasi integral. (Arsip Zenius)

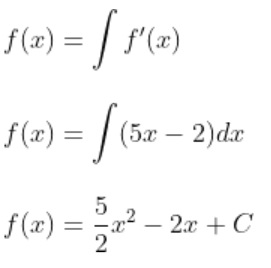
Kalau f(2) = 12, maka:

Pembahasan soal aplikasi integral. (Arsip Zenius)

Soal 2

Pembahasan

Kalau dibikin persamaan, maka:

III. TURUNAN FUNGSI ALJABAR

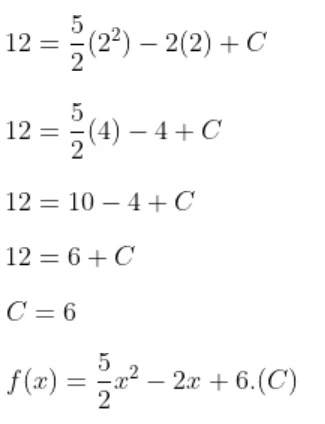
NAMA: RAISYA ALIA YUSARIN

XI IPS 1/29

MATEMATIKA SEMESTER GENAP

 A. TURUNAN FUNGSI ALJABAR DAN RUMUS TURUNAN

Pengertian Turunan Fungsi Aljabar

Turunan fungsi atau juga bisa disebut dengan diferensial adalah fungsi lain dari suatu fungsi sebelumnya, contohnya fungsi f dijadikan f' yang mempunyai nilai tidak memakai aturan dan hasil dari fungsi akan berubah sesuai dengan variabel yang dimasukan, atau secara umum suatu besaran yang berubah seiring perubahan besaran lainnya. Proses dalam menemukan turunan disebut sebagai diferensiasi. Lalu untuk pengertian turunan aljabar adalah perluasan dari materi limit fungsi.

Notasi turunan fungsi aljabar seperti berikut:

Seperti yang telah disebutkan di atas, jika turunan fungsi aljabar merupakan perluasan dari materi limit fungsi sehingga dapat didefinisikan seperti berikut:

Rumus Turunan Aljabar

Setelah memahami tentang pengertian dari turunan fungsi aljabar, hal yang perlu Sobat Pintar pelajari adalah rumus dari turunan fungsi aljabar. Rumus turunan fungsi aljabar ini terbagi menjadi beberapa rumus berikut:

Turunan Fungsi Pangkat

Turunan Hasil Kali Fungsi

Bentuk dari fungsi kali adalah f(x) = u(x) . v(x), sehingga turunannya adalah f’(x) = u’(x)v(x) + u(x)v’(x).

Turunan Fungsi Pembagian

Turunan Pangkat dari Fungsi

Turunan Trigonometri

https://akupintar.id/info-pintar/-/blogs/turunan-fungsi-aljabar-pengertian-rumus-aplikasi-contoh-soal

B. PERSAMAAN GARIS SINGGUNG KURVA MENGGUNAKAN TURUNAN

"garis singgung (disebut juga garis tangen) kurva bidang pada titik yang diketahui adalah garis lurus yang "hanya menyentuh" kurva pada titik tersebut." (wikipedia).

Dengan bahasa yang lebih sederhana dapat kita tuliskan garis singgung (tangent line) ialah garis yang hanya memiliki satu titik persekutuan (disebut sebagai titik singgung) dengan kurva.

Dengan pengertian garis singgung di atas, apakah garis pada gambar yang ketiga dibawah ini termasuk garis singgung?

Garis talibusur $AB$ atau dapat juga kita sebut dengan garis potong (secant line) yang menghubungkan titik $A$ dan $B$ pada kurva $y=f\left(x\right)$. Gradien (kemiringan) garis potong $AB$ adalah:
$\begin{array}{cc}{m}_{AB}& =\frac{\Delta y}{\Delta x}\\ & =\frac{f\left(x_2\right)-f\left(x_1\right)}{x_2-x_1}\\ & =\frac{f\left(x_1+h\right)-f\left(x_1\right)}{x_1+h-x_1}\\ & =\frac{f\left(x_1+h\right)-f\left(x_1\right)}{h}\end{array}$

Jika titik $B$ kita geser mendekati titik $A$ maka $\Delta x$ atau $h$ semakin kecil yang mengakibatkan $\Delta y$ juga semakin kecil.

Apabila titik $B$ semakin mendekati $A$ atau $\Delta x=h$ sangat kecil (mendekati nol), sehingga titik $A$ dan titik $B$ seolah-olah berimpit maka diperoleh garis singgung kurva $f\left(x\right)$ di titik $A$.

Gradien garis singgung kurva di titik $A\left(x_1,f\left(x_1\right)\right)$ adalah
$\begin{array}{cc}{m}_A& =\underset{h\to 0}{lim}\frac{f\left(x_1+h\right)-f\left(x_1\right)}{h}\\ m_A& =f^{\prime }\left(x_1\right)\end{array}$

Dari penjabaran di atas, dengan bahasa yang sederhana dapat kita tuliskan bahwa untuk titik $A\left(x_1,y_1\right)$ yang terletak pada kurva $f\left(x\right)$, maka gradien garis singgung di titik $A\left(x_1,y_1\right)$ adalah $m_A=f^{\prime }\left(x_1\right)$.

Untuk penjelasan lebih lanjut mari kita simak beberapa contoh soal berikut:

* Contoh pertama: *
tentukan gradien garis singgung kurva $f\left(x\right)=x^2–6x+5$ di titik $A(6,5)$
Jawab:
Sebagai tahap awal perlu diperhatikan apakah titik $A(6,5)$ terletak pada kurva $f\left(x\right)$. Untuk mengetahuinya kita periksa apakah $f\left(6\right)=5$,
$\begin{array}{cc}f\left(x\right)& =x^2–6x+5\\ f\left(6\right)& =6^2–6\left(6\right)+5\\ & =36–36+5\\ & =5\end{array}$
Dari hasil di atas kita ketahui bahwa titik $A(6,5)$ terletak pada kurva $f\left(x\right)$.
Seperti disampaikan sebelumnya bahwa pada titik $A\left(x_1,y_1\right)$ gradien garis singgung adalah $m_A=f^{\prime }\left(x_1\right)$.
Sehingga pada titik $A(6,5)$, gradien garis singgung adalah:
$\begin{array}{cc}{m}_A& =f^{\prime }\left(x_1\right)\\ f\left(x\right)& =x^2–6x+5\\ f^{\prime }\left(x\right)& =2x–6\\ m_A& =2x_1-6\\ & =2\left(6\right)-6\\ & =12-6=6\end{array}$

* Contoh kedua: *
tentukan gradien garis singgung kurva $f\left(x\right)=x^3–2x$ di titik $B(2,4)$
Jawab:
Sebagai tahap awal perlu diperhatikan apakah titik $B(2,4)$ terletak pada kurva $f\left(x\right)$. Untuk mengetahuinya kita periksa apakah $f\left(2\right)=4$,
$\begin{array}{cc}f\left(x\right)& =x^3–2x\\ f\left(2\right)& =2^3–2\left(2\right)\\ & =8–4\\ & =4\end{array}$
Dari hasil di atas kita ketahui bahwa titik $B(2,4)$ terletak pada kurva $f\left(x\right)$.
Seperti disampaikan sebelumnya bahwa pada titik $B\left(x_1,y_1\right)$ gradien garis singgung adalah $m_B=f^{\prime }\left(x_1\right)$.
Sehingga pada titik $B(2,4)$, gradien garis singgung adalah:
$\begin{array}{cc}{m}_B& =f^{\prime }\left(x_1\right)\\ f\left(x\right)& =x^3–2x\\ f^{\prime }\left(x\right)& =3x^2–2\\ m_B& =3x_1^2-2x_1\\ & =3(2{)}^2-2(2)\\ & =12-4\\ & =8\end{array}$

$\begin{array}{r}\mathrm{<br>}\end{array}$

SOAL LATIHAN dan PEMBAHASAN GARIS SINGGUNG KURVA DENGAN TURUNAN

1. Soal Latihan Garis Singgung Dengan Turunan

Diketahui kurva $f\left(x\right)=3x^2–2x+1$. Gradien garis singgung kurva tersebut pada titik $T(1,2)$ adalah...

$\begin{array}{cc}\left(A\right)& 3\\ \left(B\right)& 4\\ \left(C\right)& 7\\ \left(D\right)& -2\\ \left(E\right)& -4\end{array}$

Alternatif Pembahasan:

Pada titik $A\left(a,b\right)$ gradien garis singgung adalah $m_A=f^{\prime }\left(a\right)$
$\begin{array}{cc}f\left(x\right)& =3x^2–2x+1\\ f^{\prime }\left(x\right)& =6x–2\\ & \text{gradien di titik}T(1,2)\\ m_T& =6\left(1\right)-2\\ & =4\end{array}$

$\therefore$ Pilihan yang sesuai adalah $\left(B\right)$

 https://www.defantri.com/2020/09/garis-singgung-kurva-dengan-turunan.html

C. nilai stasioner dan turunan ke 2

YYU87G