Nama: RAISYA ALIA YUSARIN
Kelas: XI IPS 1
Kamis,21 Juli 2022
Transformasi dalam matematika memiliki arti sebagai suatu fungsi yang memetakan kedudukan setiap titik dari posisi awal menjadi posisi baru. Transformasi terdiri dari empat jenis, yaitu translasi, refleksi, rotasi, dan dilatasi.
A. TRANSLASI (Pergeseran),Refleksi (Pencerminan),Rotasi (Perputaran),Dilatasi (Perkalian)
TRANSLASI (Pergeseran)
Translasi adalah pergeseran objek menurut jarak dan arah tertentu. Translasi merupakan transformasi yang memindahkan setiap titik pada suatu bidang dengan jarah dan arah yang diberikan. Dalam transformasi translasi, setiap titik dipindahkan dengan besar dan arah yang sama.
Misalnya, sebuah titik ditranslasikan sejauh a satuan sejajar sumbu X dan sejauh b satuan sejajar sumbu Y. Artinya, a merupakan gerak horizontal (positif ke kanan, negatif ke kiri), dan b adalah gerak vertikal (positif ke atas, negatif ke bawah).
Refleksi (Pencerminan)
Refleksi sering kita temukan pada permukaan cermin atau pada permukaan air yang jernih. Refleksi sendiri merupakan transformasi yang memetakan setiap titik dengan ketentuan sebagai berikut.
- Titik yang terletak pada garis cermin tidak mengalami perubahan posisi.
- Titik yang tidak terletak pada garis cermin akan dicerminkan sehingga jarak objek ke cermin sama dengan jarak bayangan ke cermin.
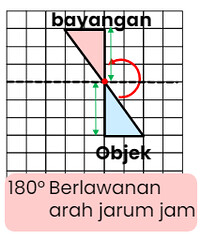
Untuk memahami sifat-sifat refleksi, perhatikan gambar di bawah ini.
Dari gambar tersebut, kita dapat menyimpulkan bahwa bayangan hasil pencerminan yang terletak di belakang garis cermin berhadapan dengan objek. Garis putus-putus yang menghubungkan titik bayangan dan titik objek tegak lurus dengan garis cermin. Kemudian, kita juga menemukan bahwa panjang ruas garis dan besar sudut bayangan sama dengan panjang ruas garis dan besar sudut objek. Objek dan bayangannya memiliki bentuk dan ukuran yang sama, tapi terletak pada arah yang berlawanan.
Rotasi (Perputaran)
Bentuk transformasi dalam matematika selanjutnya adalah rotasi. Kita bisa menemukan rotasi dalam kehidupan sehari-hari, misalnya roda yang bergerak pada porosnya, perpindahan jarum jam, dan pergerakan pintu ketika dibuka dan ditutup.
Rotasi adalah transformasi yang mengubah koordinat suatu titip terhadap titik tetap dengan besar tertentu dan arah tertentu. Arah rotasi dapat searah jarum jam atau berlawanan arah jarum jam. Sudut bernilai positif berarti berlawanan arah jarum jam, sementara sudut yang bernilai negatif berarti searah jarum jam.
Titik tetap adalah titik sudut rotasi, disebut juga dengan titik pusat rotasi. Sudut putar yang diukur berdasarkan titik pusat disebut sudut rotasi. Untuk memahami sifat-sifat rotasi, perhatikan gambar di bawah ini.
Koordinat bayangan hasil rotasi dapat ditentukan jika diketahui koordinat titik pusat rotasi, besar sudut rotasi, dan arah rotasi. Jika setiap titik sudut objek dirotasi dengan besar sudut rotasi yang sama, bayangan hasil rotasi memiliki bentuk, orientasi, dan ukuran yang sama dengan objek aslinya.
Objek dan bayangan berjarak sama terhadap titik pusat rotasi. Titik pusat rotasi adalah satu-satunya titik yang tidak berubah posisinya. Bisektor tegak lurus dari garis yang menghubungkan titik dan bayangan melewati pusat rotasi.
Dilatasi (Perkalian)
Bentuk transformasi dalam matematika yang terakhir adalah dilatasi. Dilatasi merupakan transformasi yang menghasilkan bayangan dengan bentuk yang mirip dengan objek asli, tapi dengan ukuran yang berbeda. Bayangan yang dihasilkan dapat lebih besar atau lebih kecil dari objek aslinya.
Perhatikan gambar anak penguin dan induk penguin di atas. Berdasarkan tinggi badannya, kita mengetahui bahwa induk penguin 5 kali lebih besar dari anak penguin. Ketika objek diperbesar, panjang semua sisi akan dikalikan dengan faktor skalanya.
Untuk memahami konsep dilatasi secara matematis, kita perlu mengetahui apa itu faktor skala dan titik pusat dilatasi. Faktor skala adalah nilai yang menentukan seberapa besar atau seberapa kecil bayangan hasil dilatasi terhadap objek aslinya. Sementara itu, titik pusat dilatasi digunakan untuk mengetahui titik acuan pengukuran jarak dalam memperbesar atau memperkecil objek.
Perhatikan gambar di bawah ini. Segitiga ABC diperbesar sehingga diperoleh segitiga A’B’C’.
Dengan begitu, kita mengetahui bahwa faktor skala pembesaran segitiga tersebut adalah 3.
B. GAMBAR TRANSLASI REFLEKSI ROTASI DAN DILATASI SERTA KOMPOSISI TRANSFORMASI
Refleksi (Pencerminan)
Bangun yang dicerminkan (refeksi) dengan cermin datar tidak mengalami perubahan bentuk dan ukuran. Jarak bangun dengan cermin (cermin datar) adalah sama dengan jarak bayangan dengan cermin tersebut.
Rumus transformasi refleksi:
Pencerminan terhadap titik O (0, 0)
Titik A(x, y) dicerminkan terhadap titik O (0, 0) menghasilkan bayangan A’(x’, y’), ditulis dengan:

Pencerminan terhadap sumbu x
Titik A(x, y) dicerminkan terhadap sumbu x menghasilkan bayangan A’(x’, y’) ditulis dengan:

Pencerminan terhadap sumbu y
Titik A(x, y) dicerminkan terhadap sumbu y menghasilkan bayangan A’(x’, y’) ditulis dengan:

Pencerminan terhadap garis y = x
Titik A(x, y) dicerminkan terhadap garis y = x menghasilkan bayangan A’(x’, y’) ditulis dengan:

Pencerminan terhadap garis y = –x
Titik A(x, y) dicerminkan terhadap garis y = –x menghasilkan bayangan A’(x’, y’) ditulis dengan:

Rotasi (Perputaran)
Bangun yang diputar (rotasi) tidak mengalami perubahan bentuk dan ukuran.
Rumus transformasi rotasi:
Titik A(x, y) diputar dengan pusat P(p, q) dan sudut α menghasilkan bayangan A‘(x‘, y‘), ditulis dengan:

Matriks rotasi dengan sudut α (berlawanan arah jarum jam) adalah:

Dilatasi (Perkalian)
Bangun yang diperbesar atau diperkecil (dilatasi) dengan skala k dapat mengubah ukuran atau tetap ukurannya tetapi tidak mengubah bentuk.
- Jika k ˃ 1 maka bangun akan diperbesar dan berletak searah terhadap pusat dilatasi dengan bangun semula.
- Jika k = 1 maka bangun tidak mengalami perubahan ukuran dan letak.
- Jika 0 ˂ k ˂ 1 maka bangun akan diperkecil dan terletak searah terhadap pusat dilatasi dengan bangun semula.
- Jika -1 ˂ k ˂ 0 maka bangun akan diperkecil dan terletak berlawanan arah terhadap pusat dilatasi dengan bangun semula.
- Jika k = -1 maka bangun tidak akan mengalami perubahan bentuk dan ukuran dan terletak berlawanan arah terhadap pusat dilatasi dengan bangun.
- Jika k ˂ -1 maka bangun akan diperbesar dan terletak berlawanan arah terhadap pusat dilatasi dengan bangun semula.
Rumus transformasi dilatasi
Titik A(x, y) dilatasi dengan pusat P(p, q) dan skala k menghasilkan bayangan A‘(x‘, y‘), ditulis dengan:

Komposisi Transformasi
Matriks komposisi translasi

Matriks komposisi refleksi

Matriks komposisi rotasi

Contoh 1 – Soal Translasi

Pembahasan:
Misalkan: T1 (a, b) maka T2 • T1 = (a + 4, b + 1), selanjutnya perhatikan proses translasi berikut.

Mencari nilai a:
3 + a + 2 = 8
a + 5 = 8
a = 8 – 5 = 3
Mencari nilai b:
-2 + b + 1 = 7
b – 1 = 7
b = 7 + 1 = 8
Jadi, nilai translasi dari T1 = (3, 8)
Jawaban: B
Contoh 2 – Soal dan Pembahasan Transformasi Geometri Refleksi
Persamaan garis 3x – y – 11 = 0 karena refleksi terhadap garis y = x, dilanjutkan oleh transformasi yang bersesuaian dengan matriks A,
Persamaan matriks A:

adalah ….
A. –2x – 7y –11 = 0
B. 2x + 7y – 11 = 0
C. –2x – 7y + 11 = 0
D. 2y – 7x + 11 = 0
E. 2x – 7y + 11 = 0
Pembahasan:
Pertama, cari hasil bayangan dari pencerminan terhadap garis y = x.
Matriks pencerminan terhadap garis y = x adalah:

Berdasarkan rumus di atas, dapat diperoleh kesimpulan bahwa x’ = y dan y’ = x. Substitusikan nilai tersebut pada persamaan 3x – y – 11 = 0 sehingga diperoleh persamaan berikut.
3x – y – 11 = 0
3y’ – x’ – 11 = 0
– x’ + 3y’ – 11 = 0
Kedua, langkah selanjutnya adalah transformasi yang bersesuaian dengan matriks A, Perhatikan langkah -langkahnya seperti pada cara berikut,

Sehingga, diperoleh dua persamaan berikut.
–3x’ + 2y’ = x’’
– x’ + y’ = y’’
Berikutnya, akan dicari persamaan yang senilai dengan x’ dan y’:
Mencari nilai x’:

Mencari nilai y’:

Subtitusi hasil x’ dan y’ di atas pada persamaan – x’ + 3y’– 11 = 0:
-x’ + 3y’ – 11 = 0
-(2y’’ – x’’) + 3( 3y’’ – x’’ ) – 11 = 0
-2y’’ + x’’ + 9y’’ – 3x’’ – 11 = 0
-2x’’ + 7y’’ – 11 = 0
2x’’ – 7y’’ + 11 = 0
Jadi, hasil akhir transformasi dari persamaan 3x – y – 11 = 0 adalah 2x – 7y + 11 = 0.
Jawaban: E
Contoh 3 – Soal dan Pembahasan Transformasi Geometri Rotasi
Hasil pencerminan garis x – 2y – 2 = 0 terhadap sumbu y dan kemudian diputar dengan R[ O(0,0), 90o ] adalah ….
A. 2x – y – 4 = 0
B. x – 2y – 4 = 0
C. x – 2y – 2 = 0
D. 2x – y + 2 = 0
E. 2x – y – 4 = 0
Pembahasan:
Hasil transformasi pencerminan terhadap sumbu y adalah:

Sehingga diperoleh x’ = – x dan y’ = y, selanjutnya substitusikan kedua nilai yang diperoleh pada persamaan x – 2y – 2 = 0.
x – 2y – 2 = 0
– x’ – 2y’ – 2 = 0
Transformasi selanjutnya adalah rotasi sebesar 90o yang berpusat di O(0, 0):

Substitusi nilai x’ = y’’ dan y’ = – x’’ pada persamaan –x’ – 2y’ – 2 = 0:
– x’ – 2y’ – 2 = 0
– y’’ – 2(–x’’) – 2 = 0
– y’’ + 2x’’ – 2 = 0
2x’’ – y’’ + 2 = 0
Jadi, hasil pencerminan garis x – 2y – 2 = 0 terhadap sumbu y dan kemudian diputar dengan R[ O(0,0), 90o ] adalah 2x – y + 2 = 0.
Jawaban: D
Contoh 4 – Soal dan Pembahasan Transformasi Geometri Dilatasi
Dilatasi yang berpusat di titik (3, 1) dengan faktor skala 3, memetakan titik (5, b) ke titik (a, 10). Maka nilai a – b adalah ….
A. 15
B. 11
C. 5
D. 4
E. 2
Pembahasan:
Dilatasi dengan pusat (3, 1) dengan faktor skala 3 akan menghasilkan matriks transformasi berikut.

Sehingga dapat diperoleh nilai a dan b:
- a = 9
- 3b – 2 = 10
3b = 12
b = 12 : 3 = 4
Jadi, nilai a – b = 9 – 4 = 5
Jawaban: C
1. Titik A(-3, 5) ditranslasikan dengan T1 (2, -7) kemudian dilanjutkan dengan translasi T2 (3, -2). Tentukan koordinat akhir titik A tersebut !
Pembahasan:

2. Jika garis x – 3y + 2 = 0 dilatasi dengan pusat P (2, 1) dan skala -3, maka cobalah tentukan bayangan dari garis tersebut.
Pembahasan:

Subtitusikan ke persamaan awalnya, sehingga menjadi:
x – 3y + 2 = 0 (sebelum subtitusi)
(-x /3 + 8/3) – 3 (-y/3 + 4/3)+ 2 = 0
–x /3 + y + 2/3 = 0 (kedua ruas dikalikan 3)
–x + 3y + 2 = 0
Jadi bayangan garis tersebut adalah –x + 3y + 2 = 0.
3. Garis x + 2 y – 5 = 0 dirotasi dengan dimana adalah rotasi dengan sudut 90º berlawanan arah jarum jam pada pusat P (2, 1). Tentukan persamaan posisi akhir garis tersebut !
Pembahasan:

Subtitusikan ke persamaan awalnya, sehingga menjadi:
x + 2 y – 5 = 0 (sebelum subtitusi)
(y + 1) + 2 (x + 3) – 5 = 0
y + 1 + 2x + 6 – 5 = 0
y + 2x + 2 = 0
Jadi persamaan posisi akhir garis tersebut adalah y + 2x + 2 = 0.
DAFTAR PUSTAKA
https://www.kelaspintar.id/blog/edutech/transformasi-dalam-matematika-seperti-apa-3665/
https://tambahpinter.com/transformasi-geometri/
https://idschool.net/sma/rumus-pada-transformasi-geometri-translasi-refleksi-rotasi-dan-dilatasi/








 adalah matriks berordo 3x3. Terdapat dua cara yang bisa dilakukan untuk mencari determinannya, yaitu menggunakan aturan Sarrus dan metode minor-kofaktor.
adalah matriks berordo 3x3. Terdapat dua cara yang bisa dilakukan untuk mencari determinannya, yaitu menggunakan aturan Sarrus dan metode minor-kofaktor.







.png?width=437&name=penyelesaian%20invers%20matriks%203x3%20(1).png)
.png?width=300&name=penyelesaian%20invers%20matriks%203x3%20(2).png)
.png?width=443&name=penyelesaian%20invers%20matriks%203x3%20(3).png)


